Правильный тетраэдр

Правильный тетраэдр
Тип	правильный многогранник
Комбинаторика
Элементы	4 грани 6 рёбер 4 вершины Χ = 2
Грани	правильные треугольники
Конфигурация вершины	3.3.3
Двойственный многогранник	тоже правильный тетраэдр
Классификация
Символ Шлефли	{3,3}
Группа симметрии	${\displaystyle T_{d}\cong S_{4}}$
Количественные данные
Длина ребра	${\displaystyle a}$
Площадь поверхности	${\displaystyle {\sqrt {3}}a^{2}}$
Объём	${\displaystyle {\frac {\sqrt {2}}{12}}a^{3}}$
Телесный угол при вершине	${\displaystyle \arccos {\frac {23}{27}}\approx 0.55129}$ ср

Тетраэдр называется правильным, если все его грани — равносторонние треугольники.

У правильного тетраэдра все двугранные углы при рёбрах и все трёхгранные углы при вершинах равны.

• Каждая его вершина является вершиной трех равносторонних треугольников. А значит, сумма плоских углов при каждой вершине будет равна ${\displaystyle \pi }$.
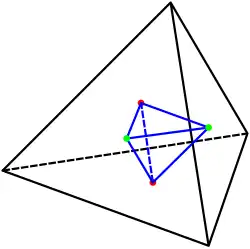
• В правильный тетраэдр можно вписать октаэдр, притом четыре из восьми граней октаэдра будут совмещены с серединными треугольниками четырёх граней тетраэдра, а все шесть вершин октаэдра будут совмещены с центрами шести рёбер тетраэдра.
  • Правильный тетраэдр с ребром ${\displaystyle x}$ состоит из одного вписанного октаэдра (в центре) с ребром ${\displaystyle {\frac {x}{2}}}$ и четырёх тетраэдров (по вершинам) с ребром ${\displaystyle {\frac {x}{2}}}$.
• Правильный тетраэдр можно вписать в куб, притом четыре вершины тетраэдра будут совмещены с четырьмя вершинами куба, а все шесть рёбер тетраэдра будут совмещены с диагоналями граней куба.

• Объём правильного тетраэдра равен ${\displaystyle V={\frac {\sqrt {2}}{12}}a^{3}}$^[1]
• Площадь поверхности равна ${\displaystyle {\sqrt {3}}a^{2}}$^[1]
• Радиус вписанной сферы равен ${\displaystyle {\frac {\sqrt {6}}{12}}a}$^[1]
• Радиус описанной сферы равен ${\displaystyle {\frac {\sqrt {6}}{4}}a}$^[1]
• Радиус полувписанной сферы равен ${\displaystyle {\frac {\sqrt {2}}{4}}a}$^[1]
• Высота правильного тетраэдра равна ${\displaystyle {\frac {\sqrt {6}}{3}}a}$ = радиус вписанной сферы + радиус описанной сферы = ${\displaystyle {\frac {\sqrt {6}}{12}}a+{\frac {\sqrt {6}}{4}}a}$
• Угол между двумя гранями равен ${\displaystyle \arccos {\frac {1}{3}}\approx 70{,}53^{\circ }}$

Точки в серединах граней правильного тетраэдра являются вершинами правильного тетраэдра.

Соотношения:

• рёбер и высот правильных тетраэдров, радиусов переписанных, описанных и писанных сфер соответственно равны ${\displaystyle {\frac {1}{3}}}$;
• площадей поверхности равно ${\displaystyle {\frac {1}{9}}}$;
• объёмов равно ${\displaystyle {\frac {1}{27}}}$.