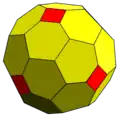
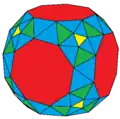
Нотация Конвея для многогранников
Нотация Конвея для многогранников, разработанная Конвеем и продвигаемая Хартом, используется для описания многогранников, опираясь на затравочный (т.е. используемый для создания других) многогранник, модифицируемый различными префикс-операциями.
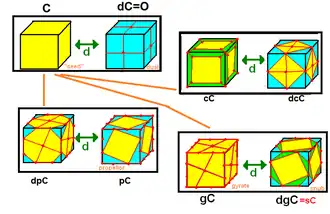
Конвей и Харт расширили идею использования операторов, подобных оператору truncation (усечения), определённого Кеплером, чтобы создавать связанные многогранники с той же симметрией. Базовые операторы могут сгенерировать все архимедовы тела и каталановы тела из правильных затравок. Например, tC представляет усечённый куб, а taC, полученный как t(aC), является усечённым октаэдром. Простейший оператор dual (двойственный) меняет местами вершины и грани. Так, двойственным многогранником для куба является октаэдр — dC=O. Применённые последовательно, эти операторы позволяют сгенерировать многие многогранники высокого порядка. Получающиеся многогранники будут иметь фиксированную топологию (вершины, рёбра, грани), в то время как точная геометрия не ограничивается.
Затравочные многогранники, являющиеся правильными многогранниками, представляются первой буквой в их (английском) названии (Tetrahedron = тетраэдр, Octahedron = октаэдр, Cube = куб, Icosahedron = икосаэдр, Dodecahedron = додекаэдр). Кроме того, используются призмы (Pn – от prism для n-угольных призм), антипризмы (An – от Antiprisms), купола (Un – от cupolae), антикупола (Vn) и пирамиды (Yn – от pyramid). Любой многогранник может выступать в качестве затравки, если операции могут на них быть выполнены. Например, правильногранные многогранники можно обозначить как Jn (от Johnson solids = тела Джонсона) для n=1...92.
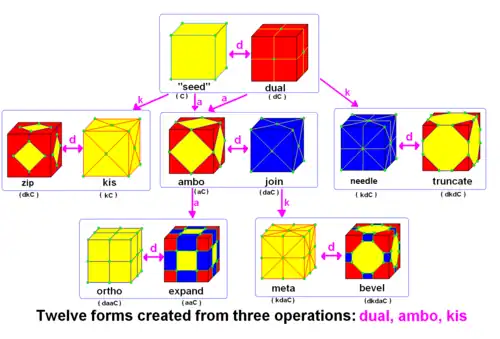
В общем случае трудно предсказать результат последовательного применения двух и более операций на заданный многогранник-затравку. Например, операция ambo, применённая дважды, оказывается той же самой, что и операция expand (расширения), aa=e, в то время как операция truncation (усечение) после операции ambo даёт то же, что и операция bevel, ta=b. Не существует общей теории, описывающей, какие многогранники могут быть получены с помощью некоторого набора операторов. Наоборот, все результаты были получены эмпирически.
Операции на многогранниках
Элементы таблицы даны для затравки с параметрами (v,e,f) (вершин, рёбер, граней), преобразуемой в новые виды в предположении, что затравка является выпуклым многогранником (топологической сферой с эйлеровой характеристикой 2). Пример, базирующийся на затравке в виде куба, дан для каждого оператора. Базовые операции достаточны для генерации зеркально симметричных однородных многогранников и их двойственных. Некоторые базовые операции можно выразить через композицию других операций.
Специальные виды
- Операция «kis» имеет вариант kn, в этом случае добавляются только пирамиды к граням с n-сторонами.
- Операция усечения имеет вариант tn, в этом случае усекаются только вершины порядка n.
Операторы применяются подобно функциям справа налево. Например, кубооктаэдр является ambo кубом (кубом, к которому применена операция ambo), то есть t(C) = aC, а усечённый кубооктаэдр равен t(a(C)) = t(aC) = taC.
Оператор хиральности
- r – «отражение» («reflect») – делает зеркальное отражение затравки. Оператор не меняет затравку, если к ней не были применены операторы s или g. Другой записью хиральной формы служит надчёркивание, например, s = rs.
Операции в таблице показаны на примере куба и нарисованы на поверхности куба. Синие грани пересекают исходные рёбра, розовые грани соответствуют исходным вершинам.
| Оператор | Пример | Название | Альтернативное построение | вершины | рёбра | грани | Описание |
|---|---|---|---|---|---|---|---|
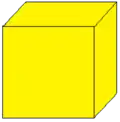 | Затравка | v | e | f | Исходный многогранник | ||
| r | reflect | v | e | f | Зеркальный образ для хиральных форм | ||
| d | 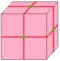 | dual | f | e | v | Двойственный многогранник для затравки – каждая вершина создаёт новую грань | |
| a | 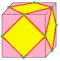 | ambo | dj djd | e | 2e | f+v | Новые вершины добавляются в середине рёбер, а старые вершины отрезаются (rectify) Операция создаёт вершины с валентностью 4. |
| j | 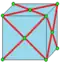 | join | da dad | v+f | 2e | e | К затравке добавляются пирамиды с достаточной высотой, так что два треугольника, принадлежащие разным пирамидам и имеющие общую сторону затравки, становятся копланарными (лежащими на одной плоскости) и образуют новую грань. Операция создаёт квадратные грани. |
| k kn | 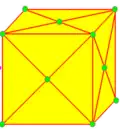 | kis | nd = dz dtd | v+f | 3e | 2e | На каждой грани добавляется пирамида. Акизация или кумуляция,[1] увеличение или пирамидальное расширение. |
| t tn | 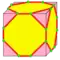 | truncate | nd = dz dkd | 2e | 3e | v+f | Отсекает все вершины. Операция является сопряжённой с kis |
| n | 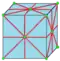 | needle | kd = dt dzd | v+f | 3e | 2e | Двойственный многогранник к усечённой затравке. Грани триангулируются с двумя треугольниками для каждого ребра. Это делит пополам грани через все вершины и рёбра, удаляя при этом исходные рёбра. Операция преобразует геодезический многогранник (a,b) в (a+2b,a-b) для a>b. Она также преобразует (a,0) в (a,a), (a,a) в (3a,0), (2,1) в (4,1), и т.д. |
| z | 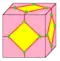 | zip | dk = td dnd | 2e | 3e | v+f | Двойственный многогранник к затравке после операции kis или усечение двойственного многогранника. Операция создаёт новые рёбра, перпендикулярные исходным рёбрам. Операция также называется bitruncation (глубоким усечением). Эта операция преобразует многогранник Голдберга G(a,b) в G(a+2b,a-b) для a>b. Она также преобразует G(a,0) в G(a,a), G(a,a) в G(3a,0), G(2,1) в G(4,1) и т.д. |
| e |  | expand (растяжение) |
aa dod = do | 2e | 4e | v+e+f | Каждая вершина создаёт новую грань, а каждое ребро создаёт новый четырёхугольник. (cantellate = скашивание) |
| o |  | ortho | daa ded = de | v+e+f | 4e | 2e | Каждая n-угольная грань делится на n четырёхугольников. |
| g rg=g | 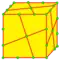 | gyro | dsd = ds | v+2e+f | 5e | 2e | Каждая n-угольная грань делится на n пятиугольников. |
| s rs=s | 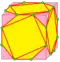 | snub | dgd = dg | 2e | 5e | v+2e+f | «расширение и кручение» – каждая вершина образует новую грань, а каждое ребро образует два новых треугольника |
| b | 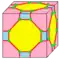 | bevel | dkda = ta dmd = dm | 4e | 6e | v+e+f | Новые грани добавляются вместо рёбер и вершин. (cantitruncation = скос-усечение) |
| m | 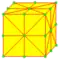 | meta medial |
kda = kj dbd = db | v+e+f | 6e | 4e | Триангуляция с добавлением вершин в центрах граней и рёбер. |
Образование правильных затравок
Все пять правильных многогранников могут быть получены из призматических генераторов, используя от нуля до двух операторов:
- Треугольная пирамида: Y3 (Тетраэдр является частным случаем пирамид)
- Треугольная антипризма: A3 (Октаэдр является частным случаем антипризм)
- O = A3
- C = dA3
- Квадратная призма: P4 (Куб является частным случаем призмы)
- C = P4
- Пятиугольная антипризма: A5
- I = k5A5 (Частный случай скрученно удлинённой бипирамиды)
- D = t5dA5 (Частный случай усечённого трапецоэдра)
Правильная евклидова мозаика может также быть использована в качестве затравки:
- Q = Quadrille (четырёхугольная мозаика) = квадратная мозаика
- H = Hextille = шестиугольная мозаика = dΔ
- Δ = Deltille = треугольная мозаика = dH
Примеры
Куб может образовать все выпуклые однородные многогранники с октаэдральной симметрией. В первой строке показаны архимедовы тела, а во второй — каталановы тела. Вторая строка образуется как двойственные многогранники к многогранникам первой строки. Если сравнивать каждый новый многогранник с кубом, можно понять визуально проведённые операции.
| Куб «затравка» | ambo | truncate | zip | expand | bevel | snub |
|---|---|---|---|---|---|---|
 C dO |
 aC aO |
 tC zO |
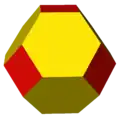 zC = dkC tO |
 aaC = eC eO |
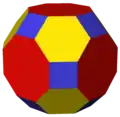 bC = taC taO |
 sC sO |
| dual | join | needle | kis | ortho | medial | gyro |
 dC O |
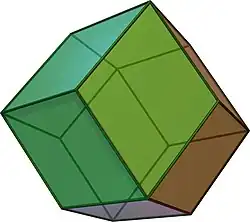 jC jO |
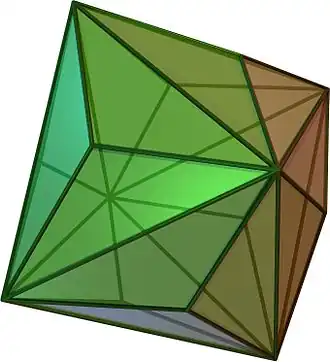 dtC = kdC kO |
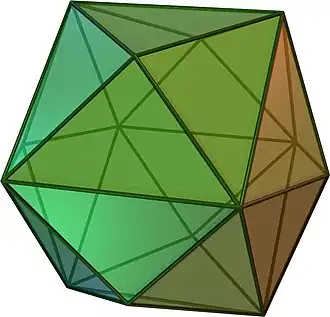 kC dtO |
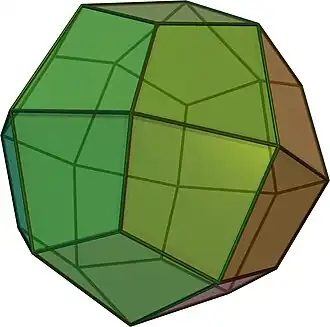 oC oO |
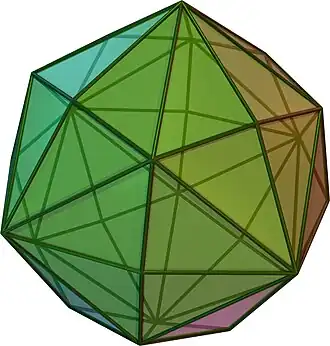 dtaC = mC mO |
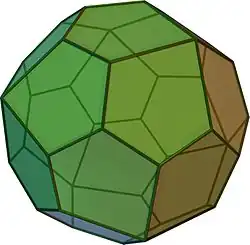 gC gO |
Усечённый икосаэдр, tI или zD, являющийся многогранником Голдберга G(2,0), создаёт дополнительные многогранники, которые ни вершинно-, ни гранетранзитивны.
| «затравка» | ambo | truncate | zip | extension | bevel | snub |
|---|---|---|---|---|---|---|
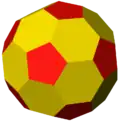 zD tI Архивная копия от 21 октября 2016 на Wayback Machine |
 azI atI Архивная копия от 1 февраля 2017 на Wayback Machine |
 tzD ttI Архивная копия от 1 февраля 2017 на Wayback Machine |
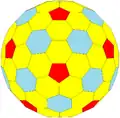 tdzD tdtI Архивная копия от 21 октября 2016 на Wayback Machine |
 aazD = ezD aatI = etI Архивная копия от 1 февраля 2017 на Wayback Machine |
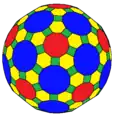 bzD btI Архивная копия от 1 февраля 2017 на Wayback Machine |
 szD stI Архивная копия от 1 февраля 2017 на Wayback Machine |
| dual | join | needle | kis | ortho | medial | gyro |
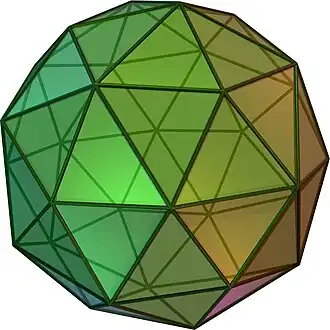 dzD dtI Архивная копия от 1 февраля 2017 на Wayback Machine |
 jzD jtI Архивная копия от 1 февраля 2017 на Wayback Machine |
 kdzD kdtI Архивная копия от 1 февраля 2017 на Wayback Machine |
 kzD ktI Архивная копия от 1 февраля 2017 на Wayback Machine |
 ozD otI Архивная копия от 1 февраля 2017 на Wayback Machine |
 mzD mtI Архивная копия от 1 февраля 2017 на Wayback Machine |
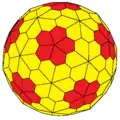 gzD gtI Архивная копия от 1 февраля 2017 на Wayback Machine |
Геометрические координаты производных форм
В общем случае затравка может считаться замощением поверхности. Поскольку операторы представляют топологические операции, то точные положения вершин производных форм в общем случае не определены. Выпуклые правильные многогранники в качестве затравки могут рассматриваться как замощения сферы, а потому производные многогранники можно рассматривать как расположенные на сфере. Подобно правильным мозаикам на плоскости, таким как шестиугольный паркет, эти многогранники на сфере могут выступать в качестве затравки для производных мозаик. Невыпуклые многогранники могут стать затравками, если связанные топологические поверхности определяются для ограничения положения вершин. Например, тороидальные многогранники могут произвести другие многогранники с точками на той же торической поверхности.
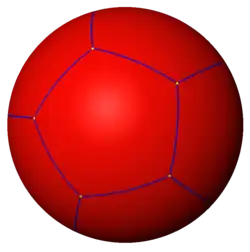 D |
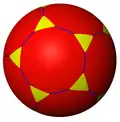 tD |
 aD |
 zD = dkD |
 eD |
 bD = taD |
 sD |
 dD |
 nD = dtD |
 jD = daD |
 kD = dtdD |
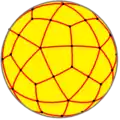 oD = deD |
 mD = dtaD |
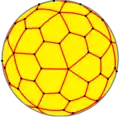 gD |
 H |
 tH |
 aH |
 tdH = H |
 eH |
 bH = taH |
 sH |
 dH |
 nH = dtH |
 jH = daH |
 dtdH = kH |
 oH = deH |
 mH = dtaH |
 gH = dsH |
Производные операции
Смешение двух и более базовых операций приводит к широкому разнообразию форм. Имеется много других производных операций. Например, смешение двух ambo, kis или expand операций вместе с операциями dual. Использование альтернативных операторов наподобие join, truncate, ortho, bevel и medial может упростить имена и удалить операторы dual. Общее число рёбер производных операций можно вычислить через мультипликаторы каждого отдельного оператора.
| Оператор(ы) | d | a j | k, t n, z | e o | g s | a&k | a&e | k&k | k&e k&a2 | e&e |
|---|---|---|---|---|---|---|---|---|---|---|
| рёберный мультипликатор | 1 | 2 | 3 | 4 | 5 | 6 | 8 | 9 | 12 | 16 |
| Уникальных производных операторов | 8 | 2 | 8 | 10 | 2 | |||||
Операции в таблице показаны для куба (в качестве примера затравки) и нарисованы на поверхности куба. Голубые грани пересекают исходные рёбра, а розовые грани соответствуют исходным вершинам.
| Оператор | Пример | Название | Альтернативное построение | вершины | рёбра | грани | Описание |
|---|---|---|---|---|---|---|---|
 | Затравка | v | e | f | Исходный многогранник | ||
| at |  | akd | 3e | 6e | v+2e+f | Операция ambo после truncate | |
| jk | 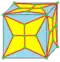 | dak | v+2e+f | 6e | 3e | Операция join после kis. Подобна ortho, за исключением того, что новые квадратные грани вставляются на место исходных рёбер | |
| ak | 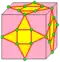 | dajd | 3e | 6e | v+2e+f | Операция ambo после kis. Подобна expand, за исключением того, что новые вершины добавляются на исходные рёбра, образуя два треугольника. | |
| jt |  | dakd = dat | v+2e+f | 6e | 3e | Операция join после truncate. Двойственный многогранник к полученному после операций truncate, затем ambo | |
| tj |  | dka | 4e | 6e | v+e+f | truncate join | |
| ka | 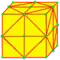 | v+e+f | 6e | 4e | kis ambo | ||
| ea or ae |  | aaa | 4e | 8e | v+3e+f | расширенная операция ambo, тройная операция ambo | |
| oa or je |  | daaa = jjj | v+3e+f | 8e | 4e | Операция ortho после ambo, тройная операция join | |
| x=kt | 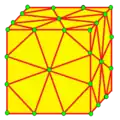 | exalt | kdkd dtkd | v+e+f | 9e | 7e | Операции kis truncate, триангуляция, деление рёбер на 3 части и добавление новых вершин в центр исходных граней. Операция преобразует геодезический многогранник (a,b) в (3a,3b). |
| y=tk | 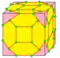 | yank | dkdk dktd | v+e+f | 9e | 7e | Операции truncate kis, расширение шестиугольниками вокруг каждого ребра Операция преобразует многогранник Голдберга G(a,b) в G(3a,3b). |
| nk |  | kdk = dtk = ktd | 7e | 9e | v+e+f | needled kis | |
| tn |  | dkdkd = dkt = tkd | 7e | 9e | v+e+f | truncate needle | |
| tt |  | dkkd | 7e | 9e | v+e+f | двойная операция truncate | |
| kk | 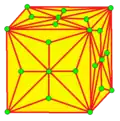 | dttd | v+2e+f | 9e | 6e | двойная операция kis | |
| nt |  | kkd = dtt | v+e+f | 9e | 7e | needle truncate | |
| tz | 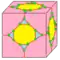 | dkk = ttd | 6e | 9e | v+2e+f | truncate zip | |
| ke | 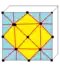 | kaa | v+3e+f | 12e | 8e | Kis expand | |
| to |  | dkaa | 8e | 12e | v+3e+f | truncate ortho | |
| ek | 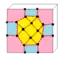 | aak | 6e | 12e | v+5e+f | expand kis | |
| ok | 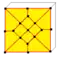 | daak = dek | v+5e+f | 12e | 6e | ortho kis | |
| et | 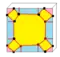 | aadkd | 6e | 12e | v+5e+f | расширенная операция truncate | |
| ot |  | daadkd = det | v+5e+f | 12e | 6e | ortho truncate | |
| te or ba | 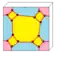 | dkdaa | 8e | 12e | v+3e+f | truncate expand | |
| ko or ma |  | kdaa = dte ma = mj | v+3e+f | 12e | 8e | kis ortho | |
| ab or am | 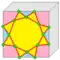 | aka = ata | 6e | 12e | v+5e+f | ambo bevel | |
| jb or jm |  | daka = data | v+5e+f | 12e | 6e | joined bevel | |
| ee |  | aaaa | v+7e+f | 16e | 8e | double-expand | |
| oo |  | daaaa = dee | 8e | 16e | v+7e+f | double-ortho |
Хиральные производные операции
Имеются другие производные операции, если используется gyro с операциями ambo, kis или expand и до трёх операций dual.
| Оператор(ы) | d | a | k | e | g | a&g | k&g | e&g | g&g |
|---|---|---|---|---|---|---|---|---|---|
| мультипликатор рёбер | 1 | 2 | 3 | 4 | 5 | 10 | 15 | 20 | 25 |
| Уникальных производных операторов | 4 | 8 | 4 | 2 | |||||
| Оператор | Пример | Название | Построение | вершин | рёбер | граней | Описание |
|---|---|---|---|---|---|---|---|
 | Затравка | v | e | f | Исходный многогранник | ||
| ag | 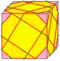 | as djsd = djs | v+4e+f | 10e | 5e | ambo gyro | |
| jg | 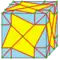 | dag = js dasd = das | 5e | 10e | v+4e+f | joined gyro | |
| ga |  | gj dsjd = dsj | v+5e+f | 10e | 4e | gyro ambo | |
| sa | 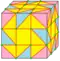 | dga = sj dgjd = dgj | 4e | 10e | v+5e+f | snub ambo | |
| kg | 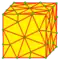 | dtsd = dts | v+4e+f | 15e | 10e | kis gyro | |
| ts | dkgd = dkg | 10e | 15e | v+4e+f | truncated snub | ||
| gk | dstd | v+8e+f | 15e | 6e | gyro kis | ||
| st | dgkd | 6e | 15e | v+8e+f | snub truncation | ||
| sk | dgtd | v+8e+f | 15e | 6e | snub kis | ||
| gt | dskd | 6e | 15e | v+8e+f | gyro truncation | ||
| ks | 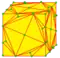 | kdg dtgd = dtg | v+4e+f | 15e | 10e | kis snub | |
| tg | dkdg dksd | 10e | 15e | v+4e+f | truncated gyro | ||
| eg | es aag | v+9e+f | 20e | 10e | expanded gyro | ||
| og | os daagd = daag | 10e | 20e | v+9e+f | expanded snub | ||
| ge | go gaa | v+11e+f | 20e | 8e | gyro expand | ||
| se | so dgaad = dgaa | 8e | 20e | v+11e+f | snub expand | ||
| gg | 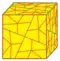 | gs dssd = dss | v+14e+f | 25e | 10e | double-gyro | |
| ss | sg dggd = dgg | 10e | 25e | v+14e+f | double-snub |
Расширенные операторы
Эти расширенные операторы нельзя создать в общем виде с помощью выше перечисленных базовых операций. Некоторые операторы могут быть созданы как частные случаи с k и t операторами, но применённые к определённым граням и вершинам. Например, куб со снятой фаской, cC, может быть построен как t4daC, как ромбододекаэдр, daC или jC с усечёнными вершинами валентности 4. Поднятый куб lC — это то же самое, что t4kC, квинтододекаэдр qD можно построить как t5daaD, t5deD или t5oD, a дельтоидальный гексеконтаэдр можно построить как deD или oD с усечением вершин с валентностью 5.
Некоторые расширенные операторы образуют последовательность и даны с последующим числом. Например, ortho делит квадратную грань на 4 квадрата, а o3 может делить на 9 квадратов. o3 является уникальным построением, в то время как o4 можно получить как oo, оператор ortho, применённый дважды. Оператор loft может включать индекс подобно оператору kis, чтобы ограничить применение на грани с указанным числом сторон.
Операция chamfer (снятие фаски) создаёт многогранник Голдберга G(2,0) с новыми шестиугольниками между исходными гранями. Последовательные операции chamfer создают G(2n,0).
| Оператор | Пример | Название | Альтернативное построение | вершин | рёбер | граней | Описание |
|---|---|---|---|---|---|---|---|
 | Затравка | v | e | f | Исходный многогранник | ||
| c (от chamfer) |  | chamfer | dud | v + 2e | 4e | f + e | Усечение рёбер. Вместо рёбер вставляются новые шестиугольные грани. Многогранник Голдберга (0,2) |
| - | 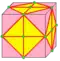 | - | dc | f + e | 4e | v + 2e | Операция dual после chamfer |
| u | 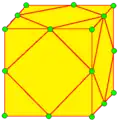 | subdivide | dcd | v+e | 4e | f+2e | Операция ambo, пока сохраняются исходные вершины Операция аналогична схеме Лупа подразделения поверхности для треугольных граней |
| - | 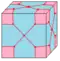 | cd | f+2e | 4e | v+e | Операция dual после subdivide | |
| l ln | 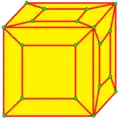 | loft | v+2e | 5e | f+2e | Расширение каждой грани призмой, добавление меньшей копии каждой грани с трапециями между внутренней и внешней гранью. | |
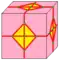 | dl dln | f+2e | 5e | v+2e | Операция dual после loft | ||
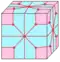 | ld lnd | f+2e | 5e | v+2e | Операция loft после dual | ||
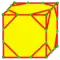 | dld dlnd | v+2e | 5e | f+2e | Операция, сопряжённая с loft | ||
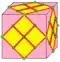 | dL0 | f+3e | 6e | v+2e | Операция dual после joined-lace | ||
 | L0d | f+2e | 6e | v+3e | Операция joined-lace после dual | ||
 | dL0d | v+3e | 6e | f+2e | Операция, сопряжённая с joined-lace | ||
| q | 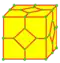 | quinto | v+3e | 6e | f+2e | Операция ortho с последующим усечением вершин, находящихся в центре исходных граней. Операция создаёт 2 новых пятиугольника для каждого исходного ребра. | |
| - |  | dq | f+2e | 6e | v+3e | Операция dual после quinto | |
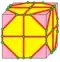 | qd | v+2e | 6e | f+3e | Операция quinto после dual | ||
| - |  | dqd | f+3e | 6e | v+2e | Операция, сопряжённая с quinto | |
| L0 |  | joined-lace | v+2e | 6e | f+3e | Аналогична операции lace, но с новыми четырёхугольными гранями на месте исходных рёбер | |
| L Ln | 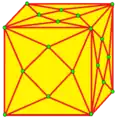 | Lace | v+2e | 7e | f+4e | Расширение каждой грани антипризмой, добавление повёрнутой меньшей копии каждой грани с треугольниками между старой и новой гранями. Индекс может быть добавлен для ограничения операции на грани с указанным числом сторон. | |
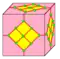 | dL dLn | f+4e | 7e | v+2e | Оператор dual после laced | ||
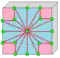 | Ld Ldn | f+2e | 7e | v+4e | Оператор lace после dual | ||
 | dLd dLnd | v+4e | 7e | f+2e | Последовательность операций dual, lace, dual | ||
| K Kn | 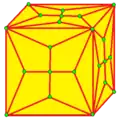 | staKe | v+2e+f | 7e | 4e | Подразделение граней с центральными чётырёхугольниками и треугольниками. Может быть добавлен индекс для ограничения операции на грани с определённым числом сторон. | |
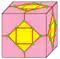 | dK dKn | 4e | 7e | v+2e+f | Операция dual после stake | ||
 | Kd | v+2e+f | 7e | 4e | Операция stake после dual | ||
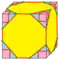 | dKd | 4e | 7e | v+2e+f | Операция, сопряжённая со stake | ||
| M3 | 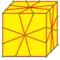 | edge-medial-3 | v+2e+f | 7e | 4e | Операция подобна m3, но не добавляются диагональные рёбра | |
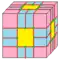 | dM3 | 4e | 7e | v+2e+f | Операция dual после edge-medial-3 | ||
 | M3d | v+2e+f | 7e | 4e | Операция edge-medial-3 после dual | ||
 | dM3d | 4e | 7e | v+2e+f | Операция, сопряжённая с edge-medial-3 | ||
| M0 | 0C.png) | joined-medial | v+2e+f | 8e | 5e | Операция подобна medial, но с добавлением ромбических граней на месте исходных рёбер. | |
0C.png) | dM0 | v+2e+f | 8e | 5e | Операция dual после joined-medial | ||
0dC.png) | M0d | v+2e+f | 8e | 5e | Операция joined-medial после dual | ||
0dC.png) | dM0d | 5e | 8e | v+2e+f | Операция, сопряжённая с joined-medial | ||
| m3 | 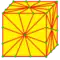 | medial-3 | v+2e+f | 9e | 7e | Триангуляция с добавлением двух вершин на каждое ребро и одной вершины в центре каждой грани. | |
| b3 | 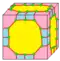 | bevel-3 | dm3 | 7e | 9e | v+2e+f | Операция dual после medial-3 |
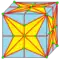 | m3d | 7e | 9e | v+2e+f | Операция medial-3 после dual | ||
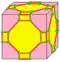 | dm3d | v+2e+f | 9e | 7e | Операция, сопряжённая с medial-3 | ||
| o3 |  | ortho-3 | de3 | v+4e | 9e | f+4e | Оператор ortho с делением рёбер на 3 |
| e3 |  | expand-3 | do3 | f+4e | 9e | v+4e | Оператор expand с делением рёбер на 3 |
| X |  | cross | v+f+3e | 10e | 6e | Комбинация операций kis и subdivide. Исходные рёбра делятся пополам и образуются треугольные и четырёхугольные грани. | |
 | dX | 6e | 10e | v+f+3e | Операция dual после cross | ||
 | Xd | 6e | 10e | v+f+3e | Операция cross после dual | ||
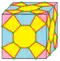 | dXd | v+f+3e | 10e | 6e | Операция, сопряжённая с cross | ||
| m4 |  | medial-4 | v+3e+f | 12e | 8e | Триангуляция с добавлением 3 вершин на каждое ребро и вершины в центр каждой грани. | |
| u5 |  | subdivide-5 | v+8e | 25e | f+16e | Рёбра делятся на 5 частей Этот оператор делит рёбра и грани так, что образуется 6 треугольников вокруг каждой новой вершины. |
Расширенные хиральные операторы
Эти операторы нельзя создать в общем виде из перечисленных выше базовых операций. Художник-геометр Харт создал операцию, которую он назвал пропеллер.
- p – «propeller» = пропеллер (оператор вращения, создающий четырёхугольники на месте вершин). Эта операция самодвойственна: dpX=pdX.
| Оператор | Пример | Название | Альтернативное построение | вершины | рёбра | грани | Описание |
|---|---|---|---|---|---|---|---|
 | «Затравка» | v | e | f | Исходный многогранник | ||
| p rp=p | 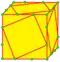 | propellor | v + 2e | 5e | f + 2e | Операция gyro, после которой выполняется ambo на вершинах в центрах исходных граней | |
| - | 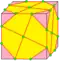 | - | dp = pd | f + 2e | 5e | v + 2e | Те же вершины, что и в gyro, но на месте исходных вершин образуются грани |
| - | 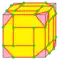 | 4e | 7e | v+2e+f | Операция подобна snub, но по периметру исходных граней идут пятиугольники, а не треугольники | ||
| - | 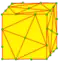 | - | - | v+2e+f | 7e | 4e | |
| w=w2=w2,1 rw=w |  | whirl | v+4e | 7e | f+2e | Операция gyro с последующим усечением вершин в центре исходных граней. Операция создаёт 2 новых шестиугольника для каждого исходного ребра, многогранник Голдберга (2,1) Производный оператор wrw преобразует G(a,b) в G(7a,7b). | |
| v rv=v | 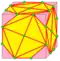 | volute | dwd | f+2e | 7e | v+4e | Оператор dual после whirl, или snub с последующей операцией kis на исходных гранях. Полученный оператор vrv преобразует геодезический многогранник (a,b) в (7a,7b). |
| g3 rg3=g3 |  | gyro-3 | v+6e | 11e | f+4e | Операция gyro создаёт 3 пятиугольника вдоль каждого исходного ребра | |
| s3 rs3=s3 | 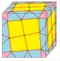 | snub-3 | dg3d = dg3 | f+4e | 11e | v+6e | Операция dual после gyro-3, операция snub, делящая рёбра на 4 срединных треугольника и с треугольниками на месте исходных вершин |
| w3,1 rw3,1=w3,1 |  | whirl-3,1 | v+8e | 13e | f+4e | Операция создаёт 4 новых шестиугольника для каждого исходного ребра, многогранник Голдберга (3,1) | |
| w3=w3,2 rw3=w3 |  | whirl-3,2 | v+12e | 19e | f+6e | Операция создаёт 12 новых шестиугольников для каждого исходного ребра, многогранник Голдберга (3,2) |
Операции, сохраняющие исходные рёбра
Эти операции расширения оставляют исходные рёбра и позволяют применять оператор к любому независимому подмножеству граней. Нотация Конвея поддерживает дополнительный индекс для этих операций, указывающий число сторон у вовлечённых в операцию граней.
| Оператор | kis | cup | acup | loft | lace | stake | kis-kis |
|---|---|---|---|---|---|---|---|
| Пример | kC | UC | VC | lC | LC | KC | kkC |
| Рёбра | 3e | 4e-f4 | 5e-f4 | 5e | 6e | 7e | 9e |
| Изображение на кубе |  | 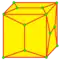 | 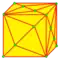 |  |  |  |  |
| Расширение | Пирамида | Купол | Антикупол | Призма | Антипризма |
Операторы Коксетера
Операторы Коксетера/Джонсона иногда полезны при смешении с операторами Конвея. Для ясности в нотации Конвея эти операции даны заглавными буквами. t-Нотация Коксетера определяет активные кружки как индексы диаграммы Коксетера — Дынкина. Таким образом, в таблице заглавная T с индексами 0,1,2 определяет однородные операторы из правильной затравки. Нулевой индекс представляет вершины, 1 представляет рёбра, а 2 представляет грани. При T = T0,1 это будет обычным усечением, а R = T1 является полным усечением, или операцией rectify, то же самое, что и оператор Конвея ambo. Например, r{4,3} или t1{4,3} является именем Коксетера для кубооктаэдра, а полноусечённый куб — это RC, то же самое, что ambo куб Конвея, aC.
| Оператор | Пример | Название | Альтернативное построение | вершины | рёбра | грани | Описание |
|---|---|---|---|---|---|---|---|
| T0 |  , t0{4,3} , t0{4,3} | «Затравка» | v | e | f | Seed form | |
| R = T1 |  , t1{4,3} , t1{4,3} | rectify | a | e | 2e | f+v | То же самое, что ambo, новые вершины добавляются в середине рёбер, а новые грани заменяют исходные вершины. Все вершины имеют валентность 4. |
| T2 |  , t2{4,3} , t2{4,3} | dual birectify |
d | f | e | v | Операция dual для затравочного многогранника — каждая вершина создаёт новую грань |
| T = T0,1 |  , t0,1{4,3} , t0,1{4,3} | truncate | t | 2e | 3e | v+f | Отсекаются все вершины. |
| T1,2 |  , t1,2{4,3} , t1,2{4,3} | bitruncate | z = td | 2e | 3e | v+f | То же самое, что и zip |
| RR = T0,2 |  , t0,2{4,3} , t0,2{4,3} | cantellate | aa=e | 2e | 4e | v+e+f | То же самое, что и expand |
| TR = T0,1,2 |  , t0,1,2{4,3} , t0,1,2{4,3} | cantitruncate | ta | 4e | 6e | v+e+f | То же самое, что и bevel |
Полуоператоры
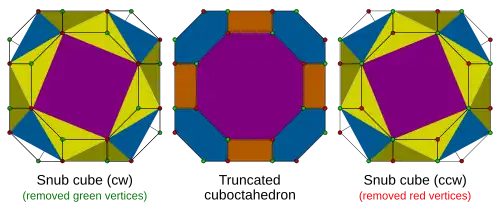
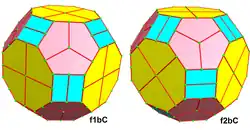
Оператор semi или demi Коксетера, H (от Half), уменьшает число сторон каждой грани вдвое, а четырёхугольные грани в двуугольники с двумя рёбрами, соединяющими две вершины, и эти два ребра могут быть заменены или не заменены одним ребром. Например, половинка куба, h{4,3}, полукуб, — это HC, представляющий один из двух тетраэдров. Ho сокращает ortho в ambo/Rectify.
Другие semi-операторы (полуоператоры) можно определить с использованием оператора H. Конвей называет оператор Snub (плосконосое усечение) Коксетера S, semi-snub (полуплосконосым усечением), определённым как Ht. Оператор snub s Конвея определяется как SR. Например, SRC — это плосконосый куб, sr{4,3}. Плосконосый октаэдр Коксетера, s{3,4} можно определить как SO, построение пиритоэдральной симметрии для правильного икосаэдра. Это также согласуется с определением правильной плосконосой квадратной антипризмой как SA4.
Оператор semi-gyro, G, определяется как dHt. Это позволяет определить оператор поворачивания Конвея g (gyro) как GR. Например, GRC — это gyro-куб, gC, или пентагональный икоситетраэдр. GO определяет пиритоэдр с пиритоэдральной симметрией, в то время как gT (gyro tetrahedron, гиротетраэдр) определяет тот же самый топологический многогранник с тетраэдральной симметрией.
Оба оператора S и G требуют, чтобы затравочный многогранник имел вершины чётной валентности. Во всех этих полуоператорах имеется два выбора для альтернации вершин для оператора half. Эти две конструкции в общем случае топологически не тождественны. Например, HjC определяет либо куб, либо октаэдр, в зависимости от того, какой набор вершин выбирается.
Другие операторы применимы только к многогранникам с гранями, имеющими чётное число рёбер. Простейшим оператором является semi-join, который является сопряжённым с оператором half, dHd.
Оператор semi-ortho, F, сопряжён с semi-snub. Он добавляет вершину в центр грани и делит пополам все рёбра, но соединяет новыми рёбрами центр только с половиной рёбер, создавая тем самым новые шестиугольные грани. Исходные квадратные грани не требуют наличия центральной вершины, а требует только одно ребро через грань, создающее пару пятиугольников. Например, двенадцатигранник тетартоид может быть построен как FC.
Оператор semi-expand, E, определяется как Htd или Hz. Оператор создаёт треугольные грани. Например, EC создаёт построение с пироэдральной симметрией псевдоикосаэдра.
| Оператор | Пример (Затравка — куб) | Название | Альтернативное построение | вершин | рёбер | граней | Описание |
|---|---|---|---|---|---|---|---|
| H = H1 H2 | 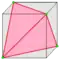 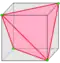 | semi-ambo Half 1 и 2 |
v/2 | e-f4 | f-f4+v/2 | Альтернирование, удаление половины вершин. Четырёхугольные грани (f4) редуцируются до одиночных рёбер. | |
| I = I1 I2 | 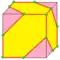 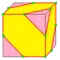 | semi-truncate 1 и 2 |
v/2+e | 2e | f+v/2 | Усекает каждую вторую вершину | |
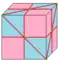 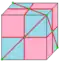 | semi-needle 1 и 2 |
dI | v/2+f | 2e | e+v/2 | Операция needle каждой второй вершины | |
| F = F1 F2 | 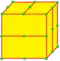 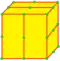 | semi-ortho Flex 1 и 2 |
dHtd = dHz dSd | v+e+f-f4 | 3e-f4 | e | Операция dual после semi-expand — создаются новые вершины на рёбрах и в центрах граней, 2n-угольники делятся на n шестиугольников, четырёхугольные грани (f4) не будут содержать центральной вершины, так что образуется две пятиугольные грани. |
| E = E1 E2 | 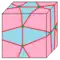 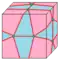 | semi-expand Eco 1 и 2 | Htd = Hz dF = Sd dGd | e | 3e-f4 | v+e+f-f4 | Операция dual после semi-ortho — создаются новые треугольные грани. Исходные грани заменяются многоугольниками с половиной сторон, четырёхугольники (f4) при этом редуцируются до одиночных рёбер. |
| U = U1 U2 |  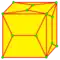 | semi-lace CUp 1 и 2 | v+e | 4e-f4 | 2e+f-f4 | Наращение граней куполами. | |
| V = V1 V2 |  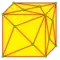 | semi-lace Anticup 3 и 4 | v+e | 5e-f4 | 3e+f-f4 | Наращение граней антикуполами | |
  | semi-medial 1 и 2 |
XdH = XJd | v+e+f | 5e | 3e | Поочерёдная операция medial относительно диагоналей | |
  | semi-medial 3 и 4 |
v+e+f | 5e | 3e | Поочерёдная операция medial относительно медиан (соединяющих середины противоположных сторон) | ||
 | semi-bevel 1 и 2 |
dXdH = dXJd | 3e | 5e | v+e+f | Поочерёдная операция bevel относительно диагоналей | |
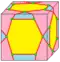 | semi-bevel 3 и 4 |
3e | 5e | v+e+f | Поочерёдная операция bevel относительно медиан |
| Оператор | Пример (Затравка — октаэдр) | Название | Альтернативное построение | вершин | рёбер | граней | Описание |
|---|---|---|---|---|---|---|---|
| J = J1 J2 |   | semi-join 1 и 2 |
dHd | v-v4+f/2 | e-v4 | f/2 | Оператор, сопряжённый с half, оператор join на чередующихся гранях. 4-валентные вершины (v4) редуцируются до 2-валентных и заменяются одним ребром. |
  | semi-kis 1 и 2 |
dId | v+f/2 | 2e | f/2+e | Операция kis на половине (поочерёдно, не соприкасающихся по ребру) граней | |
 | semi-zip 1 и 2 |
Id | f/2+e | 2e | v+f/2 | Операция zip на половине граней | |
| S = S1 S2 | 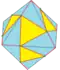  | semi-snub 1 и 2 | Ht dFd | v-v4+e | 3e-v4 | f+e | Операция dual после semi-gyro — операция snub, вращение исходных граней с добавлением новых треугольных граней в получающиеся зазоры. |
| G = G1 G2 |   | semi-gyro 1 и 2 | dHt dS = Fd dEd | f+e | 3e-v4 | v-v4+e | Операция dual после semi-snub — создаются пятиугольные и шестиугольные грани вдоль исходных рёбер. |
  | semi-medial 1 и 2 |
XdHd = XJ | 3e | 5e | v+e+f | Операция medial на половине (не соприкасающихся ребром) граней | |
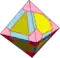 | semi-bevel 1 и 2 |
dXdHd = dXJ | v+e+f | 5e | 3e | Операция bevel на половине (не соприкасающихся ребром) граней |
Подразделения
Операция subdivision (подразделения) делит исходные рёбра на n новых рёбер, а внутренность граней заполняется треугольниками или другими многоугольниками.
Квадратное подразделение
Оператор ortho можно применить в серии степеней двойки четырёхугольных подразделений. Другие подразделения могут быть получены как результат факторизованных подразделений. Оператор propeller, применённый последовательно, даёт 5-орто подразделение. Если затравка имеет нечетырёхугольные грани, они остаются как уменьшенные копии для нечётных операторов ortho.
| Ortho | o2=o | o3 | o4=o2 | o5 =prp | o6=oo3 | o7 | o8=o3 | o9=o32 | o10=oo5 =oprp | |
|---|---|---|---|---|---|---|---|---|---|---|
| Пример |  |  |  |  |  |  |  |  |  |  |
| Вершины | v | v+e+f | v+4e | v+7e+f | v+12e | v+17e+f | v+24e | v+31e+f | v+40e | v+63e+f |
| Рёбра | e | 4e | 9e | 16e | 25e | 36e | 49e | 64e | 81e | 128e |
| Грани | f | 2e | f+4e | 8e | f+12e | 18e | f+24e | 32e | f+40e | 64e |
| Expand (dual) | e2=e | e3 | e4=e2 | e5 =dprp | e6=ee3 | e7 | e8=e3 | e9=e32 | e10=ee5 =doprp | |
| Пример |  |  |  |  |
Хиральное шестиугольное подразделение
Оператор whirl создаёт многогранник Голдберга G(2,1) с новыми шестиугольными гранями вокруг каждой исходной вершины. Две последовательные операции whirls создают G(3,5). В общем случае операция whirl может преобразовать G(a,b) в G(a+3b,2a-b) для a>b и тем же самым хиральным направлением. Если хиральные направления обратны, G(a,b) превращается в G(2a+3b,a-2b) при a>=2b и в G(3a+b,2b-a) при a<2b.
Операторы whirl-n образуют многогранники Голдберга (n,n-1) и могут быть определены путём деления рёбер затравочного многогранника на 2n-1 подрёбер.
Результат операции whirl-n и ей обратной образует (3n2-3n+1,0) многогранник Голдберга. wrw образует (7,0), w3rw3 образует (19,0), w4rw4 образует (37,0), w5rw5 образует (61,0), а w6rw6 образует (91,0). Результат двух операций whirl-n — это ((n-1)(3n-1),2n-1) или (3n2-4n+1,2n-1). Произведение wa на wb даёт (3ab-2(a+b)+1,a+b-1), а wa на обратный wb даёт (3ab-a-2b+1,a-b) для a≥b.
Произведение двух идентичных операторов whirl-n образует многогранник Голдберга ((n-1)(3n-1),2n-1). Произведение k-whirl и zip — это (3k-2,1).
| Название | Затравка | Whirl | Whirl-3 | Whirl-4 | Whirl-5 | Whirl-6 | Whirl-7 | Whirl-8 | Whirl-9 | Whirl-10 | Whirl-11 | Whirl-12 | Whirl-13 | Whirl-14 | Whirl-15 | Whirl-16 | Whirl-17 | Whirl-18 | Whirl-19 | Whirl-20 | Whirl-n |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Оператор (Состоавной) | - | w=w2 | w3 | w4 | w5 | w6 wrw3,1 | w7 | w8 w3,1w3,1 | w9 ww5,1 | w10 | w11 | w12 | w13 ww7,2 | w14 | w15 | w16 ww9,2 | w17 w3w6,1 | w18 | w19 w3,1w7,3 | w20 ww11,3 | wn |
| Многогранник Голдберга | (1,0) | (2,1) | (3,2) | (4,3) | (5,4) | (6,5) | (7,6) | (8,7) | (9,8) | (10,9) | (11,10) | (12,11) | (13,12) | (14,13) | (15,14) | (16,15) | (17,16) | (18,17) | (19,18) | (20,19) | (n,n-1) |
| T разложение |
1 | 7 | 19 | 37 | 61 | 91 7×13 | 127 | 169 13×13 | 217 7×31 | 271 | 331 | 397 | 469 7×67 | 547 | 631 | 721 7×103 | 817 19×43 | 919 | 1027 13×79 | 1141 7×163 | 3n(n-1)+1 |
| Пример |  |
 |
 |
 |
 |
 |
 |
 |
 |
||||||||||||
| Вершина | v | v+4e | v+12e | v+24e | v+40e | v+60e | v+84e | v+112e | v+144e | v+180e | v+220e | v+264e | v+312e | v+364e | v+420e | v+480e | v+544e | v+612e | v+684e | v+760e | v+2n(n-1)e |
| Рёбра | e | 7e | 19e | 37e | 61e | 91e | 127e | 169e | 217e | 271e | 331e | 397e | 469e | 547e | 631e | 721e | 817e | 919e | 1027e | 1141e | e+3n(n-1)e |
| Грани | f | f+2e | f+6e | f+12e | f+20e | f+30e | f+42e | f+56e | f+72e | f+90e | f+110e | f+132e | f+156e | f+182e | f+210e | f+240e | f+272e | f+306e | f+342e | f+380e | f+n(n-1)e |
| wnwn | (1,0) | (5,3) | (16,5) | (33,7) | (56,9) | (85,11) | (120,13) | (161,15) | (208,17) | (261,19) | (320,21) | (385,23) | (456,25) | (533,27) | (616,29) | (705,31) | (800,33) | (901,35) | (1008,37) | (1121,39) | ((n-1)(3n-1),2n-1) |
| wnrwn | (1,0) | (7,0) | (19,0) | (37,0) | (61,0) | (91,0) | (127,0) | (169,0) | (217,0) | (271,0) | (331,0) | (397,0) | (469,0) | (547,0) | (631,0) | (721,0) | (817,0) | (919,0) | (1027,0) | (1141,0) | (1+3n(n-1),0) |
| wnz | (1,1) | (4,1) | (7,1) | (10,1) | (13,1) | (16,1) | (19,1) | (22,1) | (25,1) | (28,1) | (31,1) | (34,1) | (37,1) | (40,1) | (43,1) | (46,1) | (49,1) | (52,1) | (55,1) | (58,1) | (3n-2,1) |
Триангулированное подразделение
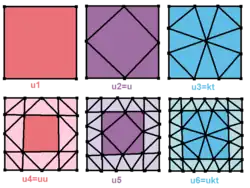
Операция un делит грани на треугольники путём деления каждого ребра на n частей, называемой n-частотным подразделением геодезического многогранника Бакминстера Фуллера[2].
Операторы Конвея на многогранниках могут построить многие из этих подразделений.
Если все исходные грани являются треугольниками, новые многогранники будут также иметь все грани в виде треугольников, и на месте исходных граней создаются треугольные мозаики. Если исходные многогранники имеют грани с бо́льшим числом сторон, все новые грани не обязательно будут треугольниками. В таких случаях к многограннику сначала можно применить операцию kis с новыми вершинами в центре каждой грани.
| Оператор | u1 | u2 =u | u3 =x | u4 =uu | u5 | u6 =ux | u7 =vrv | u8 =uuu | u9 =xx |
|---|---|---|---|---|---|---|---|---|---|
| Пример |  |
 |
 |
 |
 |
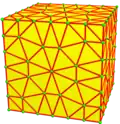 |
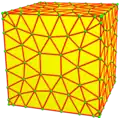 |
 |
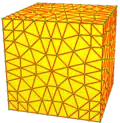 |
| Обозначение Конвея |
C Архивная копия от 2 февраля 2017 на Wayback Machine | uC Архивная копия от 15 марта 2017 на Wayback Machine | xC Архивная копия от 16 марта 2017 на Wayback Machine | uuC Архивная копия от 15 марта 2017 на Wayback Machine | u5C | uxC Архивная копия от 15 марта 2017 на Wayback Machine | vrvC Архивная копия от 15 марта 2017 на Wayback Machine | uuuC Архивная копия от 15 марта 2017 на Wayback Machine | xxC Архивная копия от 15 марта 2017 на Wayback Machine |
| Вершины | v | v+e | v+e+f | v+4e | v+8e | v+11e+f | v+16e | v+21e | v+26e+f |
| Рёбра | e | 4e | 9e | 16e | 25e | 36e | 49e | 64e | 81e |
| Грани | f | f+2e | 7e | f+8e | f+16e | 24e | f+32e | f+42e | 54e |
| Полная триангуляция | |||||||||
| Оператор | u1k | u2k =uk | u3k =xk | u4k =uuk | u5k | u6k =uxk | u7k =vrvk | u8k =uuuk | u9k =xxk |
| Пример |  |
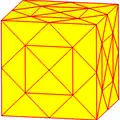 |
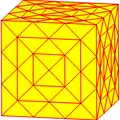 |
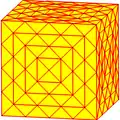 |
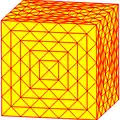 |
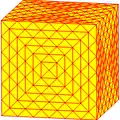 |
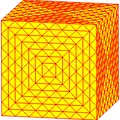 |
 |
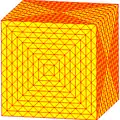 |
| Конвей | kC Архивная копия от 5 февраля 2017 на Wayback Machine | ukC Архивная копия от 15 марта 2017 на Wayback Machine | xkC Архивная копия от 15 марта 2017 на Wayback Machine | uukC Архивная копия от 16 марта 2017 на Wayback Machine | u5kC | uxkC Архивная копия от 15 марта 2017 на Wayback Machine | vrvkC Архивная копия от 15 марта 2017 на Wayback Machine | uuukC Архивная копия от 16 марта 2017 на Wayback Machine | xxkC Архивная копия от 15 марта 2017 на Wayback Machine |
| Двойственный Голдберга | {3,n+}1,1 | {3,n+}2,2 | {3,n+}3,3 | {3,n+}4,4 | {3,n+}5,5 | {3,n+}6,6 | {3,n+}7,7 | {3,n+}8,8 | {3,n+}9,9 |
Геодезические многогранники
Операции Конвея могут дублировать некоторые многогранники Голдберга и двойственные геодезическим многогранникам. Число вершин, рёбер и граней многогранника Голдберга G(m,n) можно вычислить исходя из m и n и число новых треугольников в каждом исходном треугольнике вычисляется по формуле T = m2 + mn + n2 = (m + n)2 − mn. Построения (m,0) и (m,m) перечислены ниже обозначения операций Конвея.
Класс I
Для двойственных многогранников Голдберга оператор uk определяется здесь как деление граней с подразделением рёбер на k частей. При этом оператор Конвея u = u2, а его сопряжённый оператор dud является оператором chamfer, c. Этот оператор используется в компьютерной графике, в схеме Лупа подразделения поверхности. Оператор u3 задаётся оператором Конвея kt=x, а его сопряжённый оператор y=dxd=tk. Произведение двух whirl операторов с обращением хиральности, wrw или ww, даёт 7-подразделение в виде многогранника Голдберга G(7,0), так что u7=vrv. Более мелкие подразделения и операции whirl в хиральных парах могут построить дополнительные формы класса I. Операция w(3,1)rw(3,1) даёт многогранник Голдберга G(13,0). Операция w(3,2)rw(3,2) даёт G(19,0).
| (m,0) | (1,0) | (2,0) | (3,0) | (4,0) | (5,0) | (6,0) | (7,0) | (8,0) | (9,0) | (10,0) | (11,0) | (12,0) | (13,0) | (14,0) | (15,0) | (16,0) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| T | 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 | 100 | 121 | 144 | 169 | 196 | 225 | 256 |
| Операция Составной |
u1 | u2=u =dcd |
u3=x =kt |
u4 =u22 =dccd |
u5 | u6=u2u3 =dctkd |
u7 =vv =dwrwd |
u8=u23 =dcccd |
u9=u32 =ktkt |
u10=u2u5 | u11 | u12=u22u3 =dccdkt |
u13 v3,1v3,1 |
u14=u2u7 =uvv =dcwrwd |
u15= u3u5 =u5x |
u16=u24 =dccccd |
| Треугольная грань |
||||||||||||||||
| Икосаэдр Конвей Геодезический |
 I Архивная копия от 30 декабря 2016 на Wayback Machine {3,5+}1,0 |
 uI=k5aI Архивная копия от 9 января 2017 на Wayback Machine {3,5+}2,0 |
xI=ktI Архивная копия от 30 декабря 2016 на Wayback Machine {3,5+}3,0 |
u2I Архивная копия от 9 января 2017 на Wayback Machine {3,5+}4,0 |
 {3,5+}5,0 |
 uxI Архивная копия от 9 января 2017 на Wayback Machine {3,5+}6,0 |
 vrvI Архивная копия от 9 января 2017 на Wayback Machine {3,5+}7,0 |
 u3I Архивная копия от 9 января 2017 на Wayback Machine {3,5+}8,0 |
 x2I Архивная копия от 8 января 2018 на Wayback Machine {3,5+}9,0 |
 {3,5+}10,0 |
 {3,5+}11,0 |
 u2xI Архивная копия от 10 января 2017 на Wayback Machine {3,5+}12,0 |
 {3,5+}13,0 |
 uvrvI Архивная копия от 9 января 2017 на Wayback Machine {3,5+}14,0 |
 {3,5+}15,0 |
 u4I Архивная копия от 9 января 2017 на Wayback Machine {3,5+}16,0 |
| Двойственный оператор | c | y =tk | cc | c5 | cy =ctk | ww =wrw | ccc | y2 =tktk | cc5 | c11 | ccy =cctk | w3,1w3,1 | cww =cwrw | c5y | cccc | |
| Додекаэдр Конвей Голдберг |
D Архивная копия от 30 декабря 2016 на Wayback Machine {5+,3}1,0 |
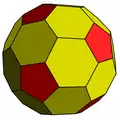 cD Архивная копия от 21 октября 2016 на Wayback Machine {5+,3}2,0 |
yD Архивная копия от 21 октября 2016 на Wayback Machine {5+,3}3,0 |
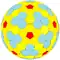 ccD Архивная копия от 21 октября 2016 на Wayback Machine {5+,3}4,0 |
c3D {5+,3}5,0 |
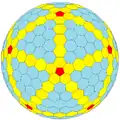 cyD Архивная копия от 21 октября 2016 на Wayback Machine {5+,3}6,0 |
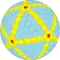 wrwD Архивная копия от 21 октября 2016 на Wayback Machine {5+,3}7,0 |
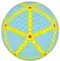 cccD Архивная копия от 21 октября 2016 на Wayback Machine {5+,3}8,0 |
 y2D Архивная копия от 30 декабря 2016 на Wayback Machine {5+,3}9,0 |
 cc5D {5+,3}10,0 |
 c11D {5+,3}11,0 |
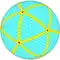 ccyD Архивная копия от 9 января 2017 на Wayback Machine {5+,3}12,0 |
 w3,1rw3,1D {5+,3}13,0 |
 cwrwD Архивная копия от 9 января 2017 на Wayback Machine {5+,3}14,0 |
 c5yD {5+,3}15,0 |
 ccccD Архивная копия от 9 января 2017 на Wayback Machine G{5+,3}16,0 |
Класс II
Может быть определено также ортогональное подразделение, используя оператор n=kd. Оператор преобразует геодезический многогранник (a,b) в (a+2b,a-b) для a>b. Он преобразует (a,0) в (a,a), а (a,a) в (3a,0). Оператор z=dk делает то же самое для многогранников Голдберга.
| (m,m) | (1,1) | (2,2) | (3,3) | (4,4) | (5,5) | (6,6) | (7,7) | (8,8) | (9,9) | (10,10) | (11,11) | (12,12) | (13,13) | (14,14) | (15,15) | (16,16) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| T= m2×3 | 3 1×3 | 12 4×3 | 27 3×3 | 48 24×3 | 75 25×3 | 108 36×3 | 147 49×3 | 192 64×3 | 243 81×3 | 300 100×3 | 363 121×3 | 432 144×3 | 507 169×3 | 588 196×3 | 675 225×3 | 768 256×3 |
| Операция | u1n n =kd |
u2n =un =dct |
u3n =xn =ktkd |
u4n =u22n =dcct |
u5n | u6n =u2=u3n =dctkt |
u7n =vvn =dwrwt |
u8n =u23n =dccct |
u9n =u32n =ktktkd |
u10n =u2u5n |
u11n | u12n =u22u3n =dcctkt |
u13n | u14n =u2u7n =dcwrwt |
u15n =u3u5n |
u16n =u24n =dcccct |
| Треугольная грань |
||||||||||||||||
| Икосаэдр Конвей Геодезический |
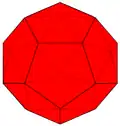 nI Архивная копия от 9 января 2017 на Wayback Machine {3,5+}1,1 |
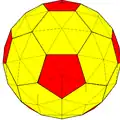 unI Архивная копия от 30 декабря 2016 на Wayback Machine {3,5+}2,2 |
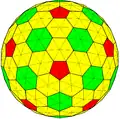 xnI Архивная копия от 9 января 2017 на Wayback Machine {3,5+}3,3 |
 u2nI Архивная копия от 30 декабря 2016 на Wayback Machine {3,5+}4,4 |
 {3,5+}5,5 |
 uxnI Архивная копия от 9 января 2017 на Wayback Machine {3,5+}6,6 |
vrvnI Архивная копия от 9 января 2017 на Wayback Machine {3,5+}7,7 |
 u3nI Архивная копия от 9 января 2017 на Wayback Machine {3,5+}8,8 |
 x2nI Архивная копия от 9 января 2017 на Wayback Machine {3,5+}9,9 |
{3,5+}10,10 |
{3,5+}11,11 |
 u2xnI Архивная копия от 10 января 2017 на Wayback Machine {3,5+}12,12 |
{3,5+}13,13 |
 dcwrwdnI Архивная копия от 9 января 2017 на Wayback Machine {3,5+}14,14 |
{3,5+}15,15 |
 u4nI {3,5+}16,16 |
| Двойственный оператор | z =dk | cz =cdk | yz =tkdk | c2z =ccdk | c5z | cyz =ctkdk | wwz =wrwdk | c3z =cccdk |
y2z =tktkdk | cc5z | c11z | c2yz =c2tkdk | c13z | cwwz =cwrwdk | c3c5z | c4z =ccccdk |
| Додекаэдр Конвей Голдберг |
 zD Архивная копия от 21 октября 2016 на Wayback Machine {5+,3}1,1 |
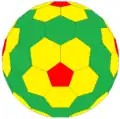 czD Архивная копия от 7 апреля 2016 на Wayback Machine {5+,3}2,2 |
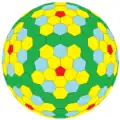 yzD Архивная копия от 30 декабря 2016 на Wayback Machine {5+,3}3,3 |
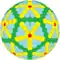 cczD Архивная копия от 7 апреля 2016 на Wayback Machine {5+,3}4,4 |
 {5+,3}5,5 |
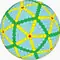 cyzD Архивная копия от 9 января 2017 на Wayback Machine {5+,3}6,6 |
 wrwzD Архивная копия от 9 января 2017 на Wayback Machine {5+,3}7,7 |
c3zD Архивная копия от 9 января 2017 на Wayback Machine {5+,3}8,8 |
y2zD Архивная копия от 9 января 2017 на Wayback Machine {5+,3}9,9 |
{5+,3}10,10 | G{5+,3}11,11 |
ccyzD Архивная копия от 9 января 2017 на Wayback Machine {5+,3}12,12 |
{5+,3}13,13 |
cwrwzD Архивная копия от 9 января 2017 на Wayback Machine G{5+,3}14,14 |
{5+,3}15,15 |
cccczD Архивная копия от 9 января 2017 на Wayback Machine {5+,3}16,16 |
Класс III
Большинство геодезических многогранников и двойственные к многогранникам Голдберга G(n,m) нельзя построить с помощью операторов, производных от операторов Конвея. Операция whirl создаёт многогранник Голдберга G(2,1) с новыми шестиугольными гранями вокруг каждой исходной вершины, а n-whirl образует G(n,n-1). На формах с икосаэдральной симметрией t5g эквивалентен в этом случае whirl. Операция v (=volute = виток, оборот) представляет треугольное подразделение, двойственное whirl. На икосаэдральных формах операция может быть осуществлена с помощью производного оператора k5s, pentakis snub.
Две последовательные операции whirl создают G(3,5). В общем случае операция whirl может преобразовать G(a,b) в G(a+3b,2a-b) для a>b с тем же самым хиральным направлением. Если хиральное направление обратное, G(a,b) становится G(2a+3b,a-2b) для a>=2b, и G(3a+b,2b-a) для a<2b.
| Операция Составная | v2,1 =v | v3,1 | v3,2=v3 | v4,1 =vn | v4,2 =vu | v5,1 | v4,3=v4 | v5,2 =v3n | v6,1 | v6,2 =v3,1u | v5,3 =vv | v7,1 =v3n | v5,4=v5 | v6,3 =vx | v7,2 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| T | 7 | 13 | 19 | 21 7×3 | 28 7×4 | 31 | 37 | 39 13×3 | 43 | 52 13×4 | 49 7×7 | 57 19×3 | 61 | 63 9×7 | 67 |
| Треугольная грань |
|||||||||||||||
| Икосаэдр Конвей Геодезический |
 vI {3,5+}2,1 |
 v3,1I {3,5+}3,1 |
 v3I {3,5+}3,2 |
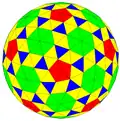 vnI Архивная копия от 3 февраля 2017 на Wayback Machine {3,5+}4,1 |
 vuI {3,5+}4,2 |
{3,5+}5,1 |
 v4I {3,5+}4,3 |
 v3nI {3,5+}5,2 |
{3,5+}6,1 |
 v3,1uI {3,5+}6,2 |
 vvI {3,5+}5,3 |
 v3nI {3,5+}7,1 |
 v5I {3,5+}5,4 |
 vxI Архивная копия от 8 января 2018 на Wayback Machine {3,5+}6,3 |
v7,2I {3,5+}7,2 |
| Оператор | w | w3,1 | w3 | wz | wc | w5,1 | w4 | w3,1z | w6,1 | w3,1c | ww | w3z | w5 | wy | w7,2 |
| Додекаэдр Конвей |
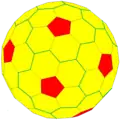 wD Архивная копия от 21 октября 2016 на Wayback Machine {5+,3}2,1 |
 w3,1D {5+,3}3,1 |
 w3D {5+,3}3,2 |
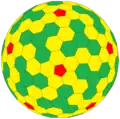 wzD Архивная копия от 21 октября 2016 на Wayback Machine {5+,3}4,1 |
 wcD Архивная копия от 21 октября 2016 на Wayback Machine {5+,3}4,2 |
 w5,1D {5+,3}5,1 |
 w4D {5+,3}4,3 |
 w3zD {5+,3}5,2 |
{5+,3}6,1 |
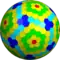 w3,1cD {5+,3}6,2 |
 wwD Архивная копия от 21 октября 2016 на Wayback Machine {5+,3}5,3 |
 w3zD {5+,3}7,1 |
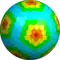 w5D {5+,3}5,4 |
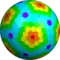 wyD Архивная копия от 8 января 2018 на Wayback Machine {5+,3}6,3 |
w7,2D {5+,3}7,2 |
| Операция Составная |
v8,1 | v6,4 =v3u |
v7,3 | v8,2 =wcz |
v6,5=v6 =vrv3,1 |
v9,1 =vv3,1 |
v7,4 | v8,3 | v9,2 | v7,5 | v10,1 =v4n |
v8,4 =vuu |
v9,3 =v3,1x |
v7,6=v7 | v8,6 v4u |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| T | 73 | 76 19×4 | 79 | 84 7×4×3 | 91 13×7 | 93 | 97 | 103 | 109 | 111 37×3 | 112 7×4×4 | 117 13×9 | 127 | 148 37×4 | |
| Треугольная грань |
|||||||||||||||
| Икосаэдр Конвей Геодезический |
v8,1I {3,5+}8,1 |
 v3uI {3,5+}6,4 |
v7,3I {3,5+}7,3 |
 vunI {3,5+}8,2 |
 vv3,1I {3,5+}6,5 |
 vrv3,1I {3,5+}9,1 |
v7,4I {3,5+}7,4 |
v8,3I {3,5+}8,3 |
v9,2I {3,5+}9,2 |
v7,5I {3,5+}7,5 |
 v4nI {3,5+}10,1 |
 vuuI {3,5+}8,4 |
 v3,1xI {3,5+}9,3 |
v7I {3,5+}7,6 |
 v4uI {3,5+}8,6 |
| Оператор | w8,1 | wrw3,1 | w7,3 | w3,1c | wcz | w3,1w | w7,4 | w8,3 | w9,2 | w7,5 | w4z | wcc | w3,1y | w7 | w4c |
| Додекаэдр Конвей |
w8,1D {5+,3}8,1 |
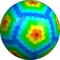 w3cD {5+,3}6,4 |
w7,3D {5+,3}7,3 |
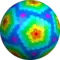 wczD {5+,3}8,2 |
 ww3,1D {5+,3}6,5 |
 wrw3,1D {5+,3}9,1 |
w7,4D {5+,3}7,4 |
w8,3D {5+,3}8,3 |
w9,2D {5+,3}9,2 |
w7,5D {5+,3}7,5 |
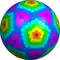 w4zD {5+,3}10,1 |
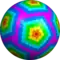 wccD {5+,3}8,4 |
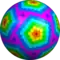 w3,1yD {5+,3}9,3 |
w7D {5+,3}7,6 |
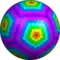 w4cD {5+,3}8,6 |
Примеры многогранников по симметрии
Повторение операций, начав с простой формы, может дать многогранники с большим числом граней, сохраняющих симметрию затравки.
Тетраэдральная симметрия
![t6dtT[англ.]](./Truncated_triakis_tetrahedron.svg.png) t6dtT
t6dtT![atT[англ.]](./Rectified_truncated_tetrahedron.png) atT
atT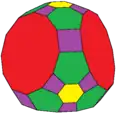 tatT
tatT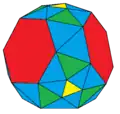 stT
stT XT (10e)
XT (10e) dXT (10e)
dXT (10e)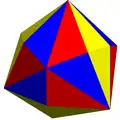 m3T
m3T b3T
b3T dHccC
dHccC dFtO
dFtO FtO
FtO
Октаэдральная симметрия

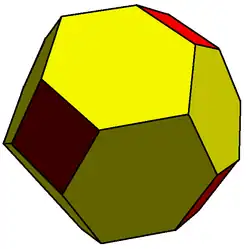
![dcC[англ.] (4e) * Архивная копия от 4 января 2017 на Wayback Machine](./Tetrakis_cuboctahedron.png)
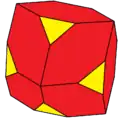
![akC[англ.] (6e) * Архивная копия от 4 января 2017 на Wayback Machine](./Rectified_truncated_octahedron.png)

 m3C (6e)
m3C (6e) m3O (6e)
m3O (6e) b3C (6e)
b3C (6e) b3O (6e)
b3O (6e)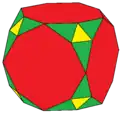
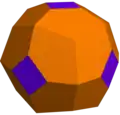 qC (6e)
qC (6e)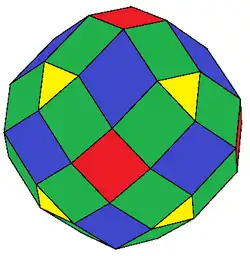
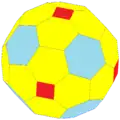
![taaC[англ.] (12e) * Архивная копия от 4 января 2017 на Wayback Machine](./Truncated_rhombicuboctahedron.png)
 XO (10e)
XO (10e) XC (10e)
XC (10e) dXO (10e)
dXO (10e) dXC (10e)
dXC (10e)
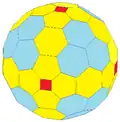
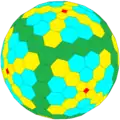
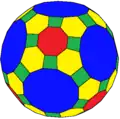
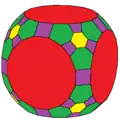


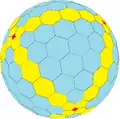
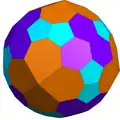 H1taC
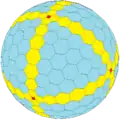
H1taC H2taC
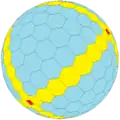
H2taC dH1taC
dH1taC dH2taC
dH2taC
- Хиральные
Изоэдральная симметрия
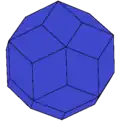



![t5daD[англ.] = cD (4e) * Архивная копия от 3 марта 2017 на Wayback Machine](./Truncated_rhombic_triacontahedron.png)
![dcI[англ.] (4e) * Архивная копия от 3 марта 2017 на Wayback Machine](./Pentakis_icosidodecahedron.png)
![dakD[англ.] (6e) * Архивная копия от 3 марта 2017 на Wayback Machine](./Rhombic_enneacontahedron.png)
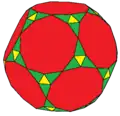
![atI[англ.] = akD (6e) * Архивная копия от 3 марта 2017 на Wayback Machine](./Rectified_truncated_icosahedron.png)

 m3D (6e)
m3D (6e) m3I (6e)
m3I (6e) b3D (6e)
b3D (6e)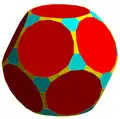 b3I (6e)
b3I (6e)


 XI (10e)
XI (10e) XD (10e)
XD (10e) dXI (10e)
dXI (10e) dXD (10e)
dXD (10e)![teD[англ.] (12e) * Архивная копия от 3 марта 2017 на Wayback Machine](./Truncated_rhombicosidodecahedron.png)

 m3aI (12e)
m3aI (12e)
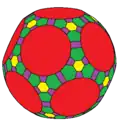

 m3tD (18e)
m3tD (18e)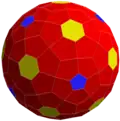

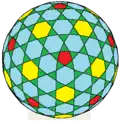






 dHtmD
dHtmD F1taD
F1taD F2taD
F2taD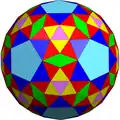 dF1taD
dF1taD dF2taD
dF2taD
- Хиральные
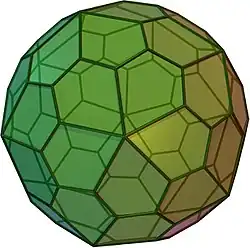 dsD (5e)
dsD (5e) sD (5e)
sD (5e) wD (7e)
wD (7e)![k5sD[англ.] (7e)](./Conway_polyhedron_K5sI.png) k5sD (7e)
k5sD (7e) saD (10e)
saD (10e)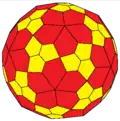 saD (10e)
saD (10e) g3D (11e)
g3D (11e) s3D (11e)
s3D (11e) g3I (11e)
g3I (11e) s3I (11e)
s3I (11e) stI (15e)
stI (15e)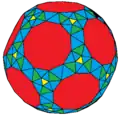 stD (15e)
stD (15e) wtI (21e)
wtI (21e) k5k6stI (21e)
k5k6stI (21e)
Диэдральная симметрия
 t4daA4=cA4
t4daA4=cA4 t4daA4=cA4 (side)
t4daA4=cA4 (side) t4daA4=cA4 (top)
t4daA4=cA4 (top)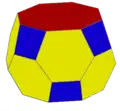 tA4
tA4 tA5
tA5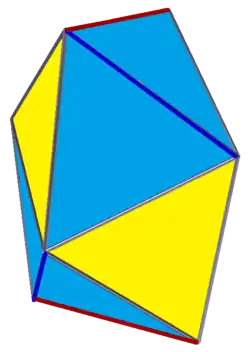 htA2
htA2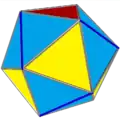 htA3=I
htA3=I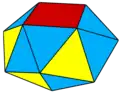 htA4
htA4 htA5
htA5 eP3 = aaP3
eP3 = aaP3 eA4 = aaA4
eA4 = aaA4
Тороидальная симметрия
Тороидальные мозаики существуют на плоском торе, на поверхности дуоцилиндра в четырёхмерном пространстве, но могут быть спроектированы в трёхмерное пространство как обычный тор. Эти мозаики топологически подобны подмножествам мозаик евклидовой плоскости.
 1x1 правильный квадратный тор, {4,4}1,0
1x1 правильный квадратный тор, {4,4}1,0 Правильный 4x4 квадратный тор, {4,4}4,0
Правильный 4x4 квадратный тор, {4,4}4,0 tQ24×12 проекция на тор
tQ24×12 проекция на тор taQ24×12 проекция на тор
taQ24×12 проекция на тор actQ24×8 проекция на тор
actQ24×8 проекция на тор tH24×12 проекция на тор
tH24×12 проекция на тор taH24×8 проекция на тор
taH24×8 проекция на тор kH24×12 проекция на тор
kH24×12 проекция на тор
Евклидова квадратная симметрия
 tQ
tQ cQ
cQ akQ
akQ HdXQ
HdXQ dHdXQ
dHdXQ
Евклидова треугольная симметрия
 tH
tH cΔ
cΔ cH
cH ctH
ctH dakH
dakH aaaH
aaaH aaaH, равносторонняя
aaaH, равносторонняя
См. также
- Однородные многогранники
- Алгоритмы компьютерной графики:
- Подразделение поверхности Ду — Сабина – expand operator
- Алгоритм подразделения поверхности Катмулла — Кларка – оператор ortho
- Многогранник Годберга
- Симметрогранник
Примечания
- ↑ Cumulation - from Wolfram MathWorld. Дата обращения: 25 октября 2017. Архивировано 24 ноября 2017 года.
- ↑ Pugh, 1976, с. 63.
Литература
- George W. Hart, Sculpture based on Propellorized Polyhedra, Proceedings of MOSAIC 2000, Seattle, WA, August, 2000, pp. 61–70 Архивная копия от 3 ноября 2017 на Wayback Machine
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass. Chapter 21: Naming the Archimedean and Catalan polyhedra and Tilings // The Symmetries of Things. — 2008. — ISBN 978-1-56881-220-5.
- Visualization of Conway Polyhedron Notation // World Academy of Science, Engineering and Technology 50. — 2009.
- Anthony Pugh. Chapter 6, Geodesic polyhedral // Polyhedra: a visual approach. — 1976. — С. p.63.
Ссылки
- George Hart's Conway interpreter Архивная копия от 29 ноября 2014 на Wayback Machine: generates polyhedra in VRML, taking Conway notation as input. Also includes helpful explanations of the operations.
- Polyhedra Names Архивная копия от 12 ноября 2020 на Wayback Machine
- Vertex- and edge-truncation of the Platonic and архимедовых тел leading to vertex-transitive polyhedra Архивная копия от 16 марта 2019 на Wayback Machine Livio Zefiro
- polyHédronisme Архивная копия от 25 апреля 2012 на Wayback Machine: generates polyhedra in HTML5 canvas, taking Conway notation as input
- Weisstein, Eric W. Conway Polyhedron Notation (англ.) на сайте Wolfram MathWorld.
- John Conway's notation Архивная копия от 3 февраля 2018 на Wayback Machine Visualization of Conway Polyhedron Notation Архивная копия от 9 апреля 2017 на Wayback Machine
- Weisstein, Eric W. Truncation (англ.) на сайте Wolfram MathWorld. (truncate)
- Weisstein, Eric W. Rectification (англ.) на сайте Wolfram MathWorld. (ambo)
- Weisstein, Eric W. Cumulation or Apiculation (англ.) на сайте Wolfram MathWorld. (kis)
- Conway operators, PolyGloss, Wendy Krieger Архивная копия от 22 октября 2017 на Wayback Machine
- Derived Solids