| Логистическое распределение |
|---|
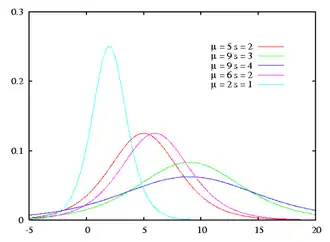 Плотность вероятности Плотность вероятности |
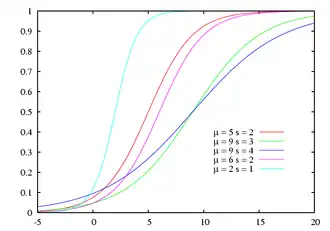 Функция распределения Функция распределения |
| Обозначение |
 |
| Параметры |

 |
| Носитель |
;+\infty )}
 |
| Плотность вероятности |
 |
| Функция распределения |
 |
| Математическое ожидание |
 |
| Медиана |
 |
| Мода |
 |
| Дисперсия |
 |
| Коэффициент асимметрии |
 |
| Коэффициент эксцесса |
 |
| Дифференциальная энтропия |
 |
| Производящая функция моментов |

для  , Бета-функция , Бета-функция |
| Характеристическая функция |

для  |
Логисти́ческое распределе́ние в теории вероятностей и математической статистике — один из видов абсолютно непрерывных распределений. Формой напоминает нормальное распределение, но имеет более «тяжёлые» концы и больший коэффициент эксцесса.
Определение
Функция плотности
Функция плотности вероятности логистического распределения задаётся формулой:


Альтернативная параметризация задается подстановкой  . Тогда функция плотности имеет вид:
. Тогда функция плотности имеет вид:

Функция распределения
Функцией распределения является логистическая функция:


Квантили
Обратная функция к функции распределения ( ), обобщение logit-функции:
), обобщение logit-функции:

Моменты распределения
Моменты высших порядков
Центральный момент n-го порядка может быть вычислен как:
![{\displaystyle {\begin{aligned}\mathbb {E} [(X-\mu )^{n}]&=\int _{-\infty }^{\infty }(x-\mu )^{n}dF(x)=\int _{0}^{1}{\big (}F^{-1}(p)-\mu {\big )}^{n}dp\\&=s^{n}\int _{0}^{1}{\Big [}\ln \!{\Big (}{\frac {p}{1-p}}{\Big )}{\Big ]}^{n}\,dp.\end{aligned}}}](./b2c78b16b8f01233401ab078eaee073a9da1bce8.svg)
Интеграл может быть выражен через числа Бернулли:
![{\displaystyle \mathbb {E} [(X-\mu )^{n}]=s^{n}\pi ^{n}(2^{n}-2)\cdot |B_{n}|.}](./9e2689eef7599b16e9f15a2da22cea99de6c229e.svg)
Литература
- N. Balakrishnan (1992). Handbook of the Logistic Distribution. Marcel Dekker, New York. ISBN 0-8247-8587-8.
- Johnson, N. L., Kotz, S., Balakrishnan N. (1995). Continuous Univariate Distributions. Vol. 2 (2nd Ed. ed.). ISBN 0-471-58494-0.
|
|---|
| Дискретные | |
|---|
Абсолютно
непрерывные | |
|---|
 Плотность вероятности
Плотность вероятности  Функция распределения
Функция распределения