Распределение Бернулли
| Распределение Бернулли | |
|---|---|
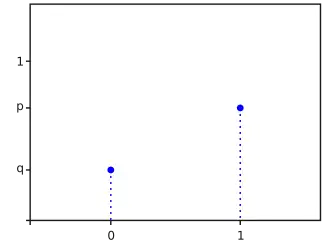 Функция вероятности Функция вероятности | |
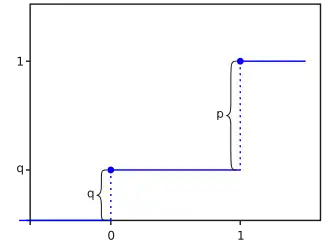 Функция распределения Функция распределения | |
| Параметры |
|
| Носитель | |
| Функция вероятности | |
| Функция распределения | |
| Математическое ожидание | |
| Мода | |
| Дисперсия | |
| Коэффициент асимметрии | |
| Коэффициент эксцесса | |
| Дифференциальная энтропия | |
| Производящая функция моментов | |
| Характеристическая функция | |
Распределе́ние Берну́лли в теории вероятностей и математической статистике — дискретное распределение вероятностей, моделирующее случайный эксперимент произвольной природы, при заранее известной вероятности успеха или неудачи.
Определение
Случайная величина имеет распределение Бернулли, если она принимает всего два значения: и с вероятностями и соответственно. Таким образом:
- ,
- .
Принято говорить, что событие соответствует «успеху», а событие — «неудаче». Эти названия условные, и в зависимости от конкретной задачи могут быть заменены на противоположные.
Свойства
Предельное свойство
Предельное свойство описывается теоремой Пуассона:
Пусть есть последовательность серий испытаний Бернулли, где — вероятность «успеха», — количество «успехов».
Тогда если
- то
Моменты распределения Бернулли
- ,
- , так как: .
Вообще, легко видеть, что
Замечание
Если независимые случайные величины , имеют распределение Бернулли с вероятностью успеха , то
имеет биномиальное распределение с степенями свободы.
См. также
Литература
- Hazewinkel, Michiel, ed. (2001), "Binomial distribution", Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4