| Распределение Фишера (Распределение Снедекора) |
|---|
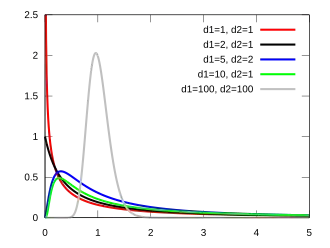 Плотность вероятности Плотность вероятности |
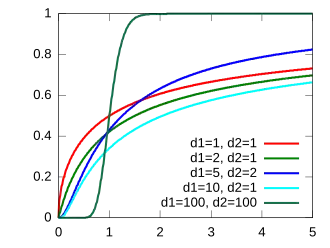 Функция распределения Функция распределения |
| Обозначение |
 |
| Параметры |
 - числа степеней свободы - числа степеней свободы |
| Носитель |
 |
| Плотность вероятности |
 |
| Функция распределения |
 |
| Математическое ожидание |
 , если , если  |
| Мода |
 , если , если  |
| Дисперсия |
 если если  |
| Коэффициент асимметрии |

если  |
| Производящая функция моментов |
не существует[1] |
Распределе́ние Фи́шера в теории вероятностей — это двухпараметрическое семейство абсолютно непрерывных распределений.
Определение
Пусть  — две независимые случайные величины, имеющие распределение хи-квадрат:
— две независимые случайные величины, имеющие распределение хи-квадрат:  , где
, где  . Тогда распределение случайной величины
. Тогда распределение случайной величины
 называется распределением Фишера (распределением Снедекора) со степенями свободы
называется распределением Фишера (распределением Снедекора) со степенями свободы  и
и  . Пишут
. Пишут  .
.
Свойства распределения Фишера
- Если
 , то
, то  .
.
- Распределение Фишера сходится к единице. Доказательство:
если  , то
, то  по распределению при
по распределению при  , где
, где  — дельта-функция в единице, то есть распределение случайной величины-константы
— дельта-функция в единице, то есть распределение случайной величины-константы  .
.
Примечания
- ↑ Johnson N. L., Kotz S., Balakrishnan N. Continuous Univariate Distributions, Volume 2 (Second Edition, Section 27).. — Wiley, 1995. — ISBN 0-471-58494-0.
Ссылки
|
|---|
| Дискретные | |
|---|
Абсолютно
непрерывные | |
|---|
 Плотность вероятности
Плотность вероятности  Функция распределения
Функция распределения