Усечённый икосаэдр

Усечённый икоса́эдр
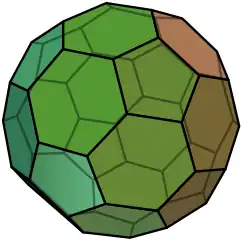Для увеличения щёлкните по картинке. Вращение фигуры
Тип	Полуправильный многогранник
Грани	пятиугольники (12), шестиугольники (20)
Граней	32
Рёбер	90
Вершин	60
Граней при вершине	3
Группа симметрии	Икосаэдрическая (Ih)
Двойственный многогранник	Пентакисдодекаэдр

Усечённый икосаэдр^[1][2][3] — многогранник, состоящий из 12 правильных пятиугольников и 20 правильных шестиугольников. Имеет икосаэдрический тип симметрии. В каждой из вершин сходятся 2 шестиугольника и пятиугольник. Каждый из пятиугольников со всех сторон окружён шестиугольниками.

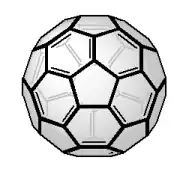
Усечённый икосаэдр — один из самых распространённых полуправильных многогранников, так как именно эту форму имеет классический футбольный мяч (если представить его пятиугольники и шестиугольники, обычно окрашенные соответственно чёрным и белым, плоскими). Эту же форму имеет молекула фуллерена C₆₀, в которой 60 атомов углерода соответствуют 60 вершинам усечённого икосаэдра.

*n32 мутации по симметрии полностью усечённых мозаик: 4.6.2n

Симметрия *n32 n,3	Сферическая				Евклидова	Компактная гиперболическая		Паракомп.	Некомпактная гиперболическая
	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]	*∞32 [∞,3]	[12i,3]	[9i,3]	[6i,3]	[3i,3]
Фигуры
Конфигурация	4.6.4	4.6.6	4.6.8	4.6.10	4.6.12	4.6.14	4.6.16	4.6.∞	4.6.24i	4.6.18i	4.6.12i	4.6.6i
Двойственная
Конфигурация грани	V4.6.4	V4.6.6	V4.6.8	V4.6.10	V4.6.12	V4.6.14	V4.6.16	V4.6.∞	V4.6.24i	V4.6.18i	V4.6.12i	V4.6.6i

Семейство однородных икосаэдральных многогранников

Симметрия: [5,3], (*532)							[5,3]+, (532)
{5,3}	t{5,3}	r{5,3}	t{3,5}	{3,5}	rr{5,3}	tr{5,3}	sr{5,3}
Двойственные к однородным многогранникам
V5.5.5	V3.10.10	V3.5.3.5	V5.6.6	V3.3.3.3.3	V3.4.5.4	V4.6.10	V3.3.3.3.5

*n32 мутации симметрий усечённых мозаик: n.6.6
Симметрия *n32 [n,3]	Сферическая		Евклидова	Компактная гиперболическая				Паракомпактная.	Некомпактная гиперболическая
	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]...	*∞32 [∞,3]	[12i,3]	[9i,3]	[6i,3]
Усечённые фигуры
Конф.	2.6.6	3.6.6	4.6.6	5.6.6	6.6.6	7.6.6	8.6.6	∞.6.6	12i.6.6	9i.6.6	6i.6.6
n-кис фигуры
Конф.	V2.6.6	V3.6.6	V4.6.6	V5.6.6	V6.6.6	V7.6.6	V8.6.6	V∞.6.6	V12i.6.6	V9i.6.6	V6i.6.6

• Звёздчатый многогранник
• Туттминкс (головоломка в форме усечённого икосаэдра)

• М. Веннинджер. Модели многогранников. — Мир, 1974.
• Многоугольники и многогранники // Энциклопедия элементарной математики. Книга четвёртая. Геометрия / Под ред. П. С. Александрова, А. И. Маркушевича, А. Я. Хинчина. — М.: Государственное издательство физико-математической литературы, 1963. — С. 382-447.
• Л. А. Люстерник. Выпуклые фигуры и многогранники. — М.: Государственное издательство технико-теоретической литературы, 1956.
• Д. Гильберт «Икосаэдр»